Théorème central limite
Théorème central limite
Pourquoi l'utiliser?
Le théorème central limite (CLT) est un fondement des tests d’hypothèses paramétriques. Comprendre ce théorème permet de mieux comprendre comment appliquer des statistiques inférentielles aux données.
Qu'est-ce que ça fait?
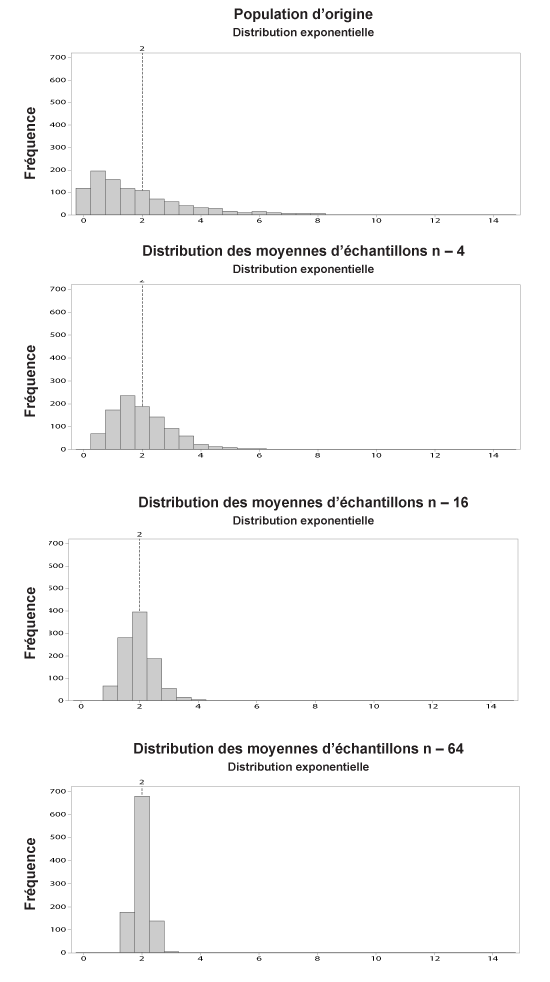
Le théorème central limite déclare que les moyennes d'échantillons aléatoires tirés de toute distribution de moyenne µ et de variance σ2 auront une distribution approximativement normale avec une moyenne égale à µ et une variance égale à σ2/n. Le CLT permet l'utilisation d'intervalles de confiance, de tests d'hypothèses, de DOE, d'analyses de régression et d'autres techniques d'analyse de données.
Comment fait-on ça?
La plupart des progiciels, tels que Minitab®, peuvent afficher des échantillons de données de distributions normales dans un graphique informatif.
Exemples :
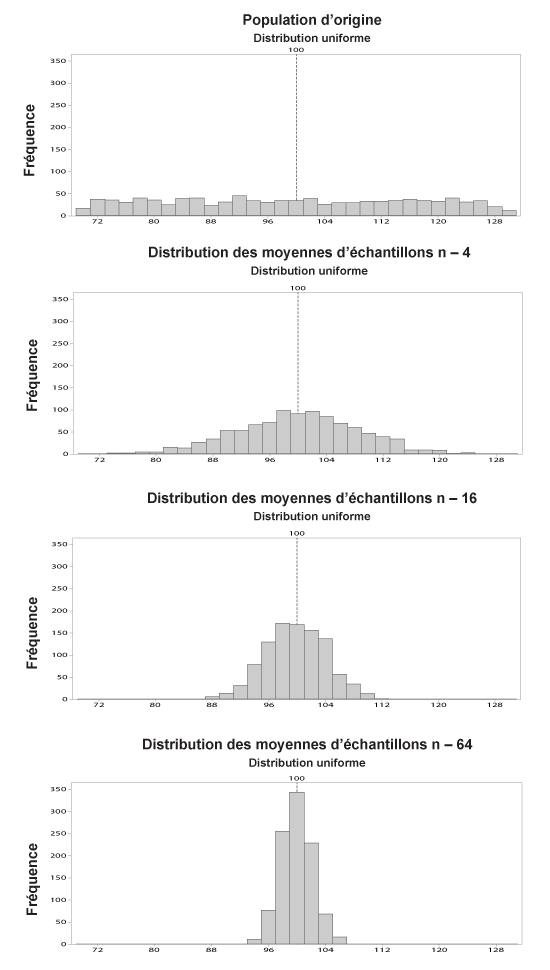
Le CLT peut être mieux compris en examinant un exemple de son application. Cet exemple prend des échantillons d'une distribution uniforme qui est une distribution non normale. Notez que lorsque la taille de l'échantillon n augmente, la variation diminue et la distribution d'échantillonnage a tendance à ressembler davantage à la distribution normale.