 Intervalles de confiance
Intervalles de confiance
Pourquoi l'utiliser?
Les intervalles de confiance aident à quantifier notre incertitude due à un échantillonnage aléatoire. Lorsque nous prenons un échantillon d'un processus, nous utilisons des statistiques pour estimer l'emplacement d'un paramètre de population. En raison de la variabilité de ces estimations statistiques due à l'échantillonnage aléatoire, nous devons quantifier notre incertitude. Les intervalles de confiance nous aident également à développer le concept de test d'hypothèse.
Qu'est-ce que ça fait?
Les intervalles de confiance fournissent des plages pour les paramètres de population (p. ex. les moyennes, les écarts types et les proportions) avec une certaine confiance. Lorsqu'une population donnée est échantillonnée plusieurs fois, les moyennes d'échantillons calculées peuvent être différentes même si la population est stable (comme illustré dans la figure suivante). Les intervalles de confiance quantifient l'incertitude en décrivant la probabilité qu'un paramètre de population se situe dans une certaine plage de valeurs. Généralement, nous calculons des intervalles de confiance de 95 %, ce qui signifie que nous sommes convaincus à 95 % que le paramètre de population se situe dans cet intervalle. Inversement, il existe un risque de 5 % (risque alpha (α) = 1 − confiance = 1−0,95 = 0,05) que le paramètre de population ne se situe pas dans l'intervalle.
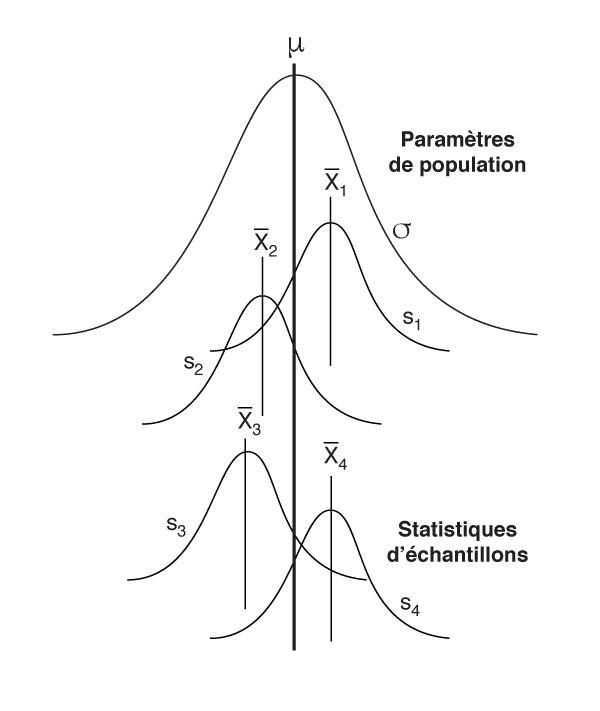
Les différences entre ces moyennes d'échantillons sont simplement dues à la nature de l'échantillonnage aléatoire. Étant donné que ces différences existent, il est essentiel d'estimer le paramètre de population réel. L'intervalle de confiance permet à l'organisation d'estimer le paramètre de population réel avec une certaine confiance.
L'intervalle de confiance est délimité par une limite inférieure et une limite supérieure qui sont déterminées par le risque associé à la formulation d'une conclusion erronée concernant le paramètre d'intérêt. Par exemple, si l'intervalle de confiance à 95 % est calculé pour un sous-groupe de données de la taille d'échantillon n, et si les limites de confiance inférieure et supérieure sont déterminées à 85,2 et 89,3 respectivement, il est possible d'indiquer avec une certitude de 95 % que la vraie moyenne de population se situe entre ces valeurs. Inversement, il existe un risque de 5 % que cet intervalle ne contienne pas la moyenne réelle de la population.
Remarque :
- Lors de l'échantillonnage d'un processus, on suppose que les échantillons sont choisis de manière aléatoire et que les sous-groupes sont indépendants.
- On ne peut pas savoir si la moyenne réelle de la population se situe dans les limites de confiance supérieure et inférieure, sauf si nous mesurons l'ensemble de la population.
- Il est extrêmement rare que nous ayons accès à des mesures pour l’ensemble de la population. La plupart des progiciels statistiques supposent que les données que nous fournissons proviennent d'un échantillon.
Comment fait-on ça?
En fonction du paramètre de population d'intérêt, les statistiques d'échantillon utilisées pour calculer l'intervalle de confiance adhèrent à différentes distributions. Des aspects de ces distributions sont utilisés dans le calcul des intervalles de confiance. La liste ci-dessous répertorie les différents intervalles de confiance, la distribution à laquelle les statistiques d'échantillon adhèrent, les formules de calcul des intervalles et un exemple de chacun. Notez comment ces intervalles de confiance sont affectés par la taille de l'échantillon, n. Des échantillons de plus grande taille entraînent des intervalles de confiance plus étroits, comme prévu par le théorème central limite. Les intervalles de confiance sont également affectés par le risque alpha. Lorsque nous augmentons le risque alpha (de 5 % à 10 %, par exemple), l'intervalle de confiance devient plus étroit.
Intervalle de confiance pour la moyenne
L'intervalle de confiance pour la moyenne utilise une distribution t et peut être calculé à l'aide de la formule suivante :
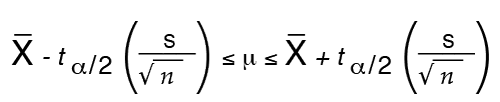
Exemple :
Un fabricant de raccords pour une application de moteur automobile souhaitait connaître, avec un degré de confiance de 90 %, la résistance moyenne des raccords en cours de fabrication. Un échantillon de 20 raccords a été sélectionné et testé sur un dynamomètre. La résistance moyenne et l'écart type de ces échantillons ont été déterminés à 167 950 et 3 590 psi, respectivement. L’intervalle de confiance pour la moyenne µ serait :
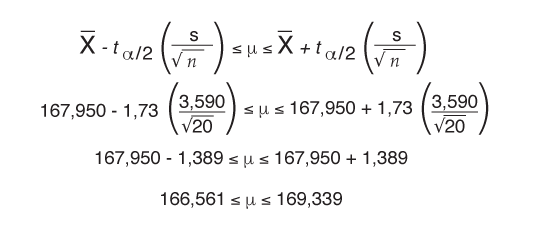
Intervalle de confiance pour l'écart type
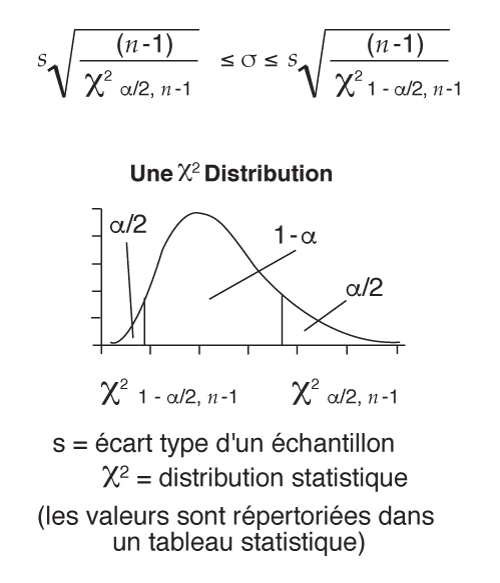
L’intervalle de confiance pour l’écart type adhère à une distribution du khi-deux et peut être calculé comme suit :
Exemple :
Un fabricant de fibres de nylon souhaite connaître, avec un degré de confiance de 95 %, l’ampleur de la variabilité de la ténacité (mesure de la résistance) d'une fibre de fil spécifique qu’il produit. Un échantillon de 14 tubes de fil a été recueilli et la ténacité moyenne et l'écart type ont été déterminés à 2,830 et 0,341 g/denier, respectivement. Pour calculer l'intervalle de confiance de 95 % pour l'écart type :
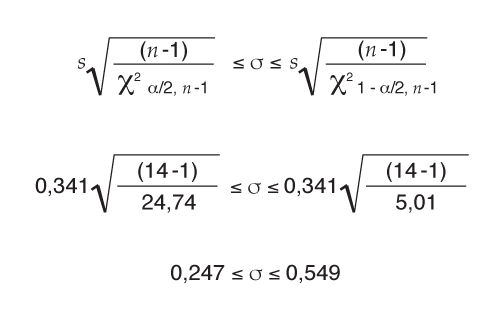
Attention : Certains logiciels et textes inverseront le sens de lecture du tableau ; donc χ2 α/2, n-1 serait 5,01, pas 24,74.
Intervalle de confiance pour la proportion de défectueux
La solution exacte pour la proportion de défectueux (p) utilise la distribution binomiale ; toutefois, dans cet exemple, l'approximation normale sera utilisée. L'approximation normale du binôme peut être utilisée lorsque np et n(1-p) sont supérieurs ou égaux à cinq. Un progiciel statistique utilisera la distribution binomiale.
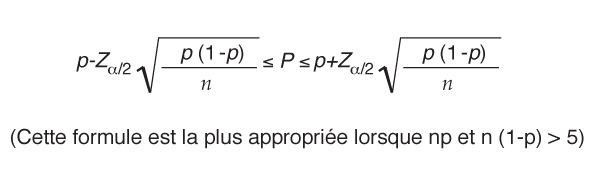
Exemple :
La solution exacte pour la proportion de défectueux (p) utilise la distribution binomiale ; toutefois, dans cet exemple, l’approximation normale sera utilisée. L’approximation normale du binôme peut être utilisée lorsque np et n(1-p) sont supérieurs ou égaux à cinq. Un progiciel statistique utilisera la distribution binomiale.
