 Régression logistique binaire
Régression logistique binaire
Pourquoi l'utiliser?
La régression logistique binaire (BLR) est utilisée pour établir une relation y = f (x) lorsque la variable dépendante (y) n'a que deux valeurs possibles. Semblable à la régression, elle explore les relations entre un ou plusieurs prédicteurs et une réponse binaire. La BLR permet à l'équipe DMAIC de prédire la probabilité que des événements futurs appartiennent à l'un ou l'autre groupe.
Qu'est-ce que ça fait?
Les prédicteurs (x) peuvent être continus ou discrets, comme pour tout problème utilisant la régression. Cependant, la variable réponse n'a que deux valeurs possibles (p. ex. succès/échec). Étant donné que l'analyse de régression nécessite une variable réponse continue qui n'est pas délimitée, ceci doit être corrigée. Ceci est accompli en convertissant d'abord la réponse des événements (p. ex. succès/échec) à la probabilité de l'un des événements, ou p. Ainsi, si p = Probabilité (succès), alors p peut prendre toute valeur comprise entre 0 et 1. Cette conversion entraîne une réponse continue, mais toujours limitée. Une transformation supplémentaire est nécessaire pour rendre la réponse à la fois continue et sans limite. Ceci s'appelle la fonction de liaison. La fonction de liaison la plus courante est la « logit », expliquée ci-dessous.
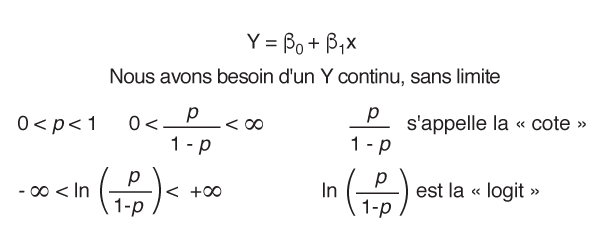
La BLR ajuste les échantillons de données à une courbe logistique en forme de S. La courbe représente la probabilité de l'événement.
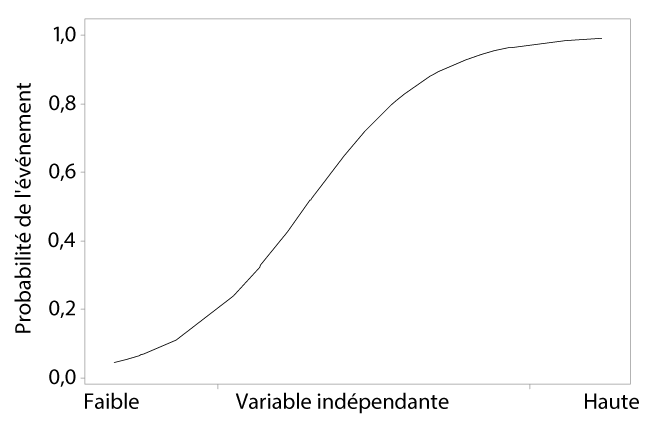
Aux faibles niveaux de la variable indépendante (x), la probabilité est proche de zéro. À mesure que le prédicteur augmente, la probabilité augmente jusqu'à un point où la pente diminue. Aux niveaux élevés de la variable indépendante, la probabilité approche 1.
Les deux exemples suivants adaptent les courbes de probabilité aux données réelles. La courbe en haut représente le « meilleur ajustement » où les probabilités inférieures à 0,5 sont codées comme un non-événement et les probabilités supérieures à 0,5 sont codées comme un événement. La courbe à travers les données, en bas, contient une zone d'incertitude où les événements et les non-événements (1 et 0) se chevauchent.
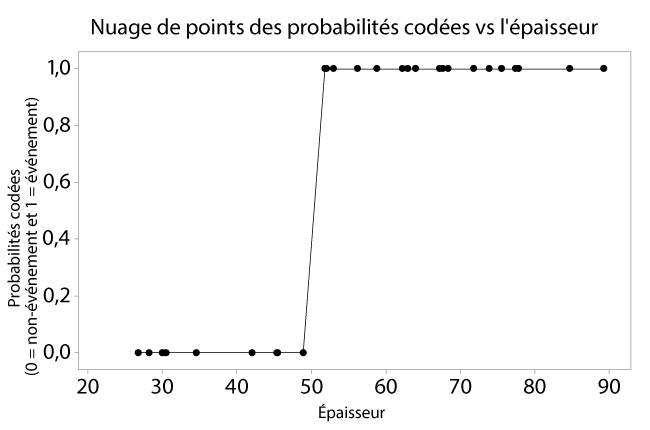
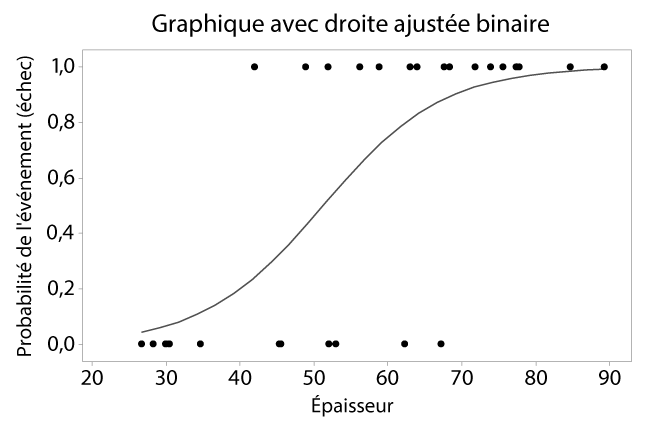
Si la probabilité d'un événement, p, est supérieure à 0,5, une régression logistique binaire prédit un « oui » pour que l'événement se produise. La probabilité qu'un événement ne se produise pas est décrite par (1-p). La probabilité, ou p/(1-p), compare la probabilité qu'un événement se produise à la probabilité qu'il ne se produise pas. La logit, ou fonction de « liaison », représente la relation entre x et y.
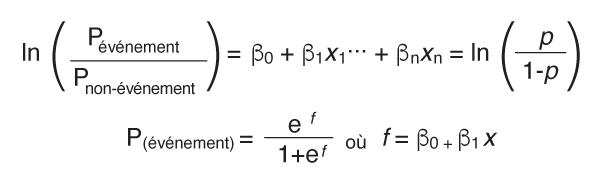
Comment fait-on ça?
- Définissez le problème et la (les) question(s) à résoudre.
- Recueillez les données appropriées dans la bonne quantité.
- Posez l'hypothèse d'un modèle (utilisez une fonction de liaison telle que logit, probit ou gompit).
- Analysez les données.
- De nombreux logiciels statistiques sont disponibles pour vous aider à analyser les données.
- Vérifiez le modèle pour la qualité de l'ajustement.
- Vérifier les résiduels pour les violations des hypothèses.
- Modifiez le modèle, si nécessaire, et répétez.
Interprétation des résultats de la BLR
La plupart des logiciels statistiques estiment les coefficients, qui représentent la modification du logit, ou ln(p/(1-p)), correspondant à une modification d'une unité dans une variable x si toutes les autres variables x sont maintenues constantes. L'un des avantages de la fonction de liaison logit est qu'elle fournit une estimation du « rapport de cotes » pour chaque prédicteur du modèle. C'est le rapport entre les « chances » avec un x particulier à une valeur de base (x0) et les « chances » si la même variable x est augmentée de 1 unité (c.-à-d. x = x0 + 1). Le « rapport de cotes » de chaque variable x est calculé directement à partir du coefficient (β) pour cet x (c.-à-d. que c'est eβ).
Les coefficients positifs signifient que la probabilité prédite de l'événement augmente à mesure que l'entrée (x) augmente. Les coefficients positifs entraînent également un rapport de cotes supérieur à 1.
Les coefficients négatifs signifient que la probabilité prédite de l'événement décroît à mesure que l'entrée (x) augmente. Les coefficients négatifs entraînent également un rapport de cotes inférieur à 1.
Un coefficient de 0 signifie qu'il n'y a aucun changement dans la probabilité prédite de l'événement lorsque l'entrée (x) augmente. Cela donne également un rapport de cotes égal à 1. Les variables dont les coefficients sont proches de 0 ou les rapports de cotes sont proches de 1 peuvent être supprimées du modèle.
Dans l'exemple suivant, les dimensions d'épaisseur de 30 écrans de verre ont été mesurées, puis les écrans ont été soumis à un test de fissuration thermique. Les articles ont été inspectés et notés comme ayant réussi ou échoué. Une valeur de 1,0 signifie que l'événement est un « échec ».

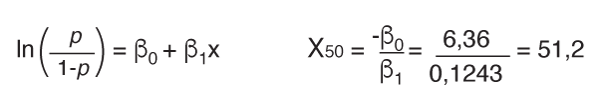

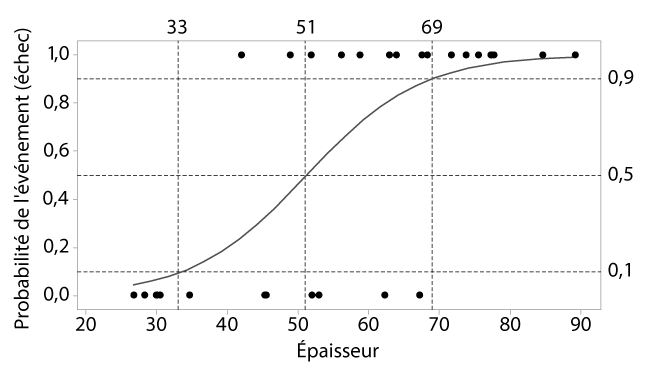
Une dimension de 51 a une probabilité d'échec de 50 %. Plus la dimension augmente, plus elle risque de provoquer un échec. Deux autres dimensions ont également été mises en évidence : une dimension de 33 n'a qu'une probabilité d'échec de 10 %, tandis qu'une dimension de 69 a une probabilité d'échec de 90 %.