Central Limit Theorem
Central Limit Theorem
Why use it?
The Central Limit Theorem (CLT) is a foundation for parametric hypothesis testing. Understanding this theorem furthers knowledge of how to apply inferential statistics to data.
What does it do?
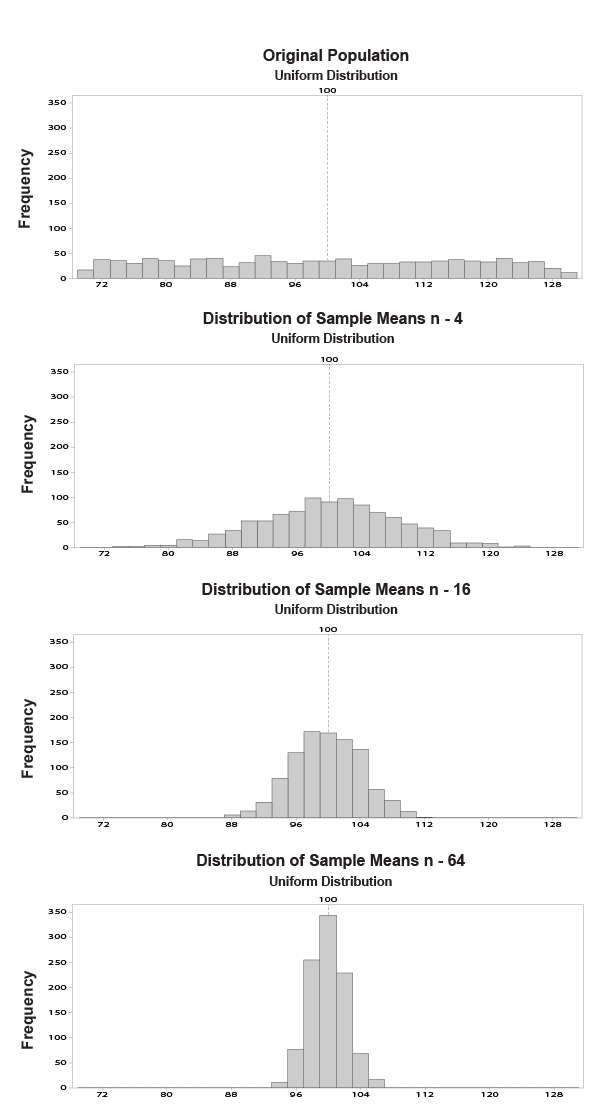
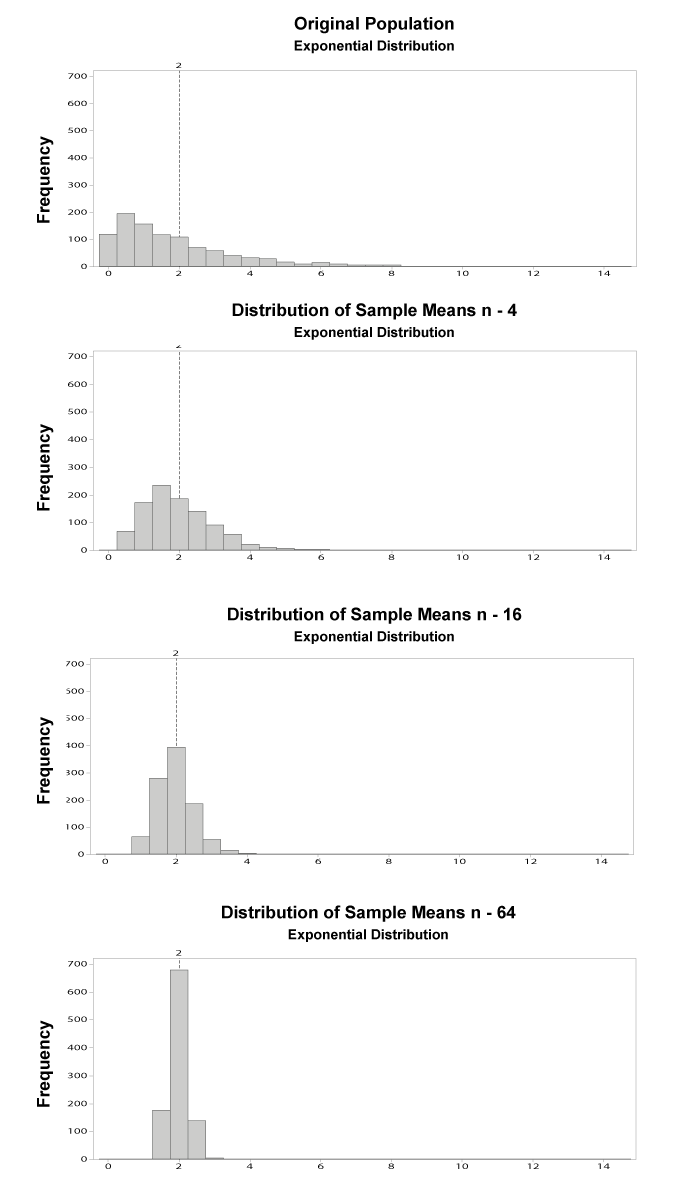
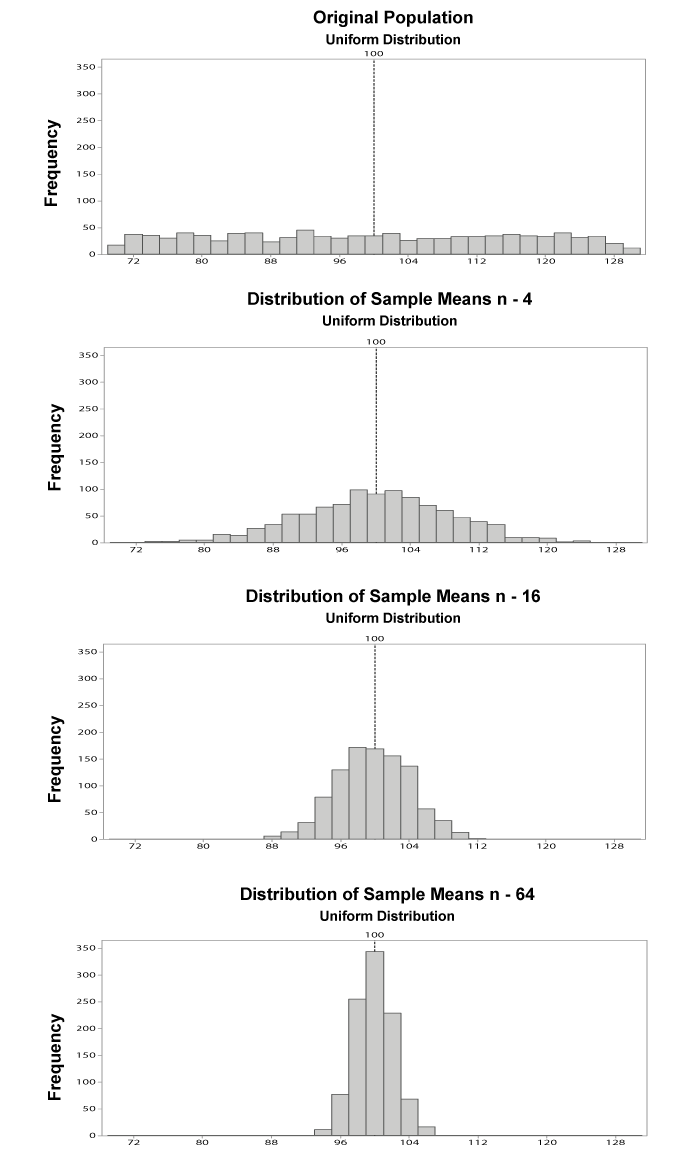
The Central Limit Theorem states that the means of random samples drawn from any distribution with mean µ and variance σ2 will have an approximately normal distribution with a mean equal to µ and a variance equal to σ2/n. The CLT allows the use of confidence intervals, hypothesis testing, DOE, regression analysis, and other analytical techniques on data.
How do I do it?
Most software packages, such as Minitab® can display data samples from normal distributions in an informative graphic.
Example:
The CLT can be better understood by reviewing an example of its application. This example takes samples from a uniform distribution which is a non-normal distribution. Notice that as the sample size n increases, the variation decreases and the sampling distribution tends to look more like the normal distribution.